

Of course on typesetting, they look almost similar, but.
Degree of freedom in statistics how to#
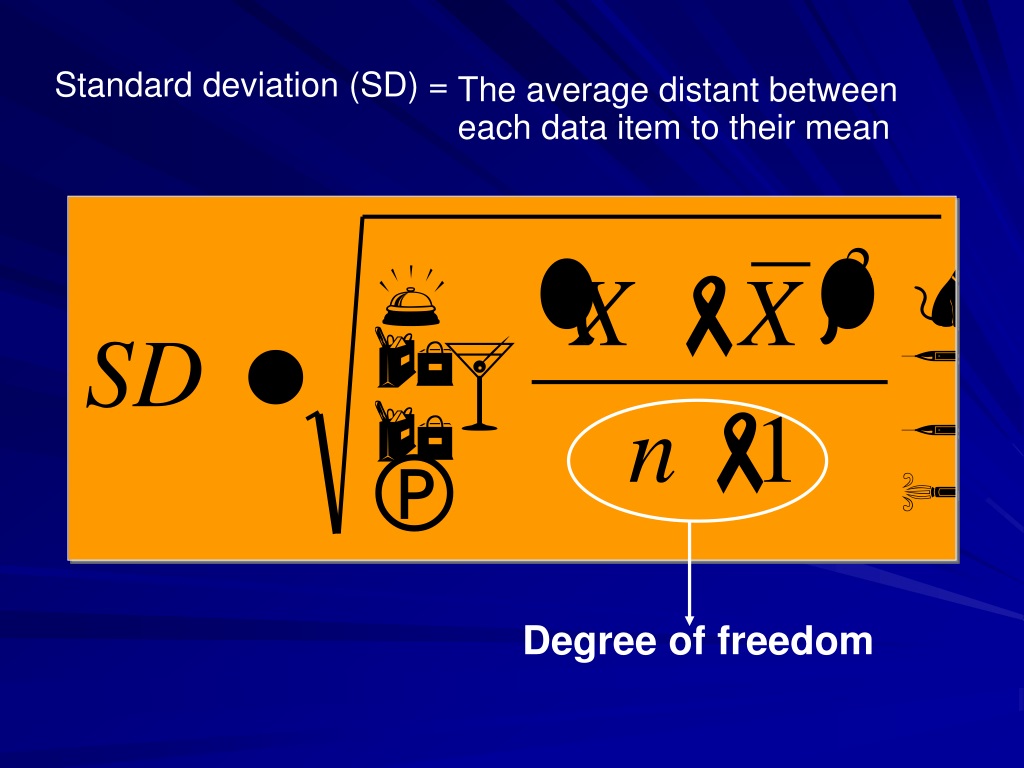
For example, imagine you have four numbers (a, b, c and d) that must add up to a total of m you are free to choose the first three numbers at random, but the fourth must be chosen so that it makes the total equal to m - thus your degree of freedom is three.Ĭopyright © 2000-2016 StatsDirect Limited, all rights reserved. Degrees of freedom (statistics), the number of values in the final calculation of a statistic that are free to vary Degrees of freedom problem, the problem of controlling motor movement given abundant degrees of freedom See also Look up degrees of freedom in Wiktionary, the free dictionary. How to denote the df (degree of freedom), particularly for t, F and 2 distributions in hypothesis testing Some references state it as the English letter v such as this one, and in Miller and Freunds Probability and Statistics for Engineers, it is denoted as Greek letter (nu). When this principle of restriction is applied to regression and analysis of variance, the general result is that you lose one degree of freedom for each parameter estimated prior to estimating the (residual) standard deviation.Īnother way of thinking about the restriction principle behind degrees of freedom is to imagine contingencies. The estimate of population standard deviation calculated from a random sample is: Thus, degrees of freedom are n-1 in the equation for s below: With 4 degrees of freedom, for example, probabilities are accurate to the fourth decimal place with 5. At this point, we need to apply the restriction that the deviations must sum to zero. Accuracy increases as degrees of freedom increase. In other words, we work with the deviations from mu estimated by the deviations from x-bar. The number of degrees of freedom of each type possessed by a molecule depends on both the number of atoms in the molecule and the geometry of the molecule, with. Thus, mu is replaced by x-bar in the formula for sigma. For example, if the variance,, is to be estimated from a random sample of N independent scores, then the degrees of freedom is equal to the number of. In order to estimate sigma, we must first have estimated mu.
The population values of mean and sd are referred to as mu and sigma respectively, and the sample estimates are x-bar and s.
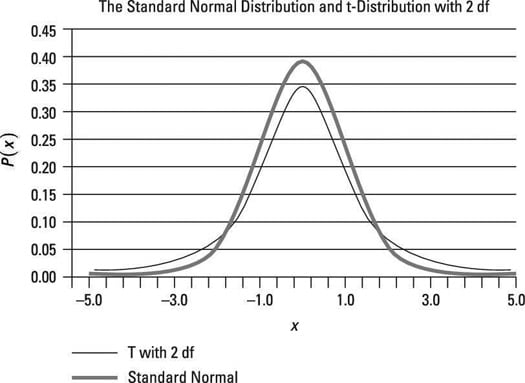
the standard normal distribution has a mean of 0 and standard deviation (sd) of 1. It is the purpose of this paper to discuss and define the statistical aspects of degrees of freedom and thereby clarify the meaning of the term. Normal distributions need only two parameters (mean and standard deviation) for their definition e.g. Introduction THE CONCEPT of 'degrees of freedom' has a very simple nature, but this simplicity is not generally exemplified in statistical textbooks. Let us take an example of data that have been drawn at random from a normal distribution. Think of df as a mathematical restriction that needs to be put in place when estimating one statistic from an estimate of another. "Degrees of freedom" is commonly abbreviated to df. The concept of degrees of freedom is central to the principle of estimating statistics of populations from samples of them. Open topic with navigation Degrees of Freedom


 0 kommentar(er)
0 kommentar(er)
